여러 숫자들로부터 다양한 조합을 만들어내는 것은 수학적 퍼즐과도 같습니다. 여기서는 8개의 숫자를 가지고 6개의 숫자로 완전 조합을 만드는 방법에 대해 알아보겠습니다.
이는 특히 로또, 퍼즐 게임, 데이터 샘플링 등에서 유용하게 활용될 수 있습니다. 6개의 숫자로 가능한 모든 조합을 만드는 방법을 설명하겠습니다.
1. 숫자의 조합
숫자의 조합은 여러 분야에서 중요한 역할을 합니다.
예를 들어 로또 번호를 고르거나, 통계학에서 샘플링할 때, 혹은 데이터 분석에서 다양한 시나리오를 검토할 때 조합의 개념이 필요합니다.
8개의 숫자를 선택하고, 이 중에서 6개의 숫자로 조합을 만드는 것은 수학적으로 흥미로운 문제입니다. 우리는 이 문제를 해결하기 위해 조합론(combinatorics)을 사용합니다.
조합론은 주어진 집합에서 특정 크기의 부분집합을 선택하는 방법을 연구하는 수학의 한 분야입니다.

2. 조합의 기본 개념
조합은 순서에 상관없이 특정 크기의 부분집합을 선택하는 것입니다.
예를 들어, {1, 2, 3}에서 2개의 숫자를 선택하는 경우, 가능한 조합은 {1, 2}, {1, 3}, {2, 3} 이렇게 세 가지입니다.
이는 수학적으로 "3C2"라고 표현하며, 이는 "3개 중에서 2개를 고르는 방법의 수"를 의미합니다.
조합의 수는 다음과 같은 공식으로 계산할 수 있습니다.
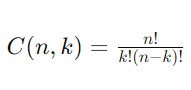
여기서 n은 전체 숫자의 개수, k는 선택할 숫자의 개수, 그리고 !는 팩토리얼(factorial)을 의미합니다.
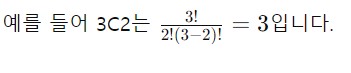
3. 로또확률
만약 처음 선택한 숫자들 안에 당첨 숫자 6개가 포함되어 있다면, 1등을 포함하여 5개 숫자 당첨 12개와 4개 숫자 당첨 15개를 보장받게 되십니다.
만약 선택한 숫자들 안에 당첨 숫자 5개가 포함되어 있다면, 5개 숫자 당첨 3개와 4개 숫자 당첨 15개, 3개 숫자 당첨 10개를 보장받게 되십니다.
만약 선택한 숫자들 안에 당첨 숫자 4개가 포함되어 있다면, 4개 숫자 당첨 6개와 3개 숫자 당첨 16개를 보장받게 되십니다.
만약 선택한 숫자들 안에 당첨 숫자 3개가 포함되어 있다면, 3개 숫자 당첨 10개를 보장받게 되십니다.
이와 같은 의미를 보다 쉽게 설명드리면, 처음 선택하신 숫자들 안에 특정 개수의 당첨 숫자가 포함되어 있을 경우 다양한 등수의 당첨을 보장받게 된다는 것입니다.
6개의 당첨 숫자가 포함되어 있다면 1등과 여러 개의 5개, 4개 숫자 당첨을 보장받게 되며, 5개의 당첨 숫자가 포함되어 있다면 여러 개의 5개, 4개, 3개 숫자 당첨을 보장받게 됩니다.
마찬가지로, 4개의 당첨 숫자가 포함되어 있다면 여러 개의 4개와 3개 숫자 당첨을, 3개의 당첨 숫자가 포함되어 있다면 여러 개의 3개 숫자 당첨을 보장받게 되는 것입니다.
로또확률은 엄청나게 낮습니다.
로또확률 6/45 : 8,145,060
8개 완전조합확률 8/45 : 290,895
8개 완전조합은 28개니까 28*290,895=8,145,060
운 좋으면 빨리걸리고 운이 조금이라도 있으면 늦게라도 걸리고 운이 나쁘면 이번 생에는 안 걸릴 수도 있습니다.
그냥 기부하는 마음으로 재미 삼아 소액으로 하는 것이 몸과 정신건강에 좋을 것 같습니다.
4. 8개의 숫자로 6개의 조합 만들기
이제 8개의 숫자로 6개의 숫자를 선택하는 방법을 구체적으로 살펴보겠습니다.
8개의 숫자를 {1, 2, 3, 4, 5, 6, 7, 8}로 가정하면, 이 중에서 6개의 숫자를 선택하는 조합의 수는 다음과 같이 계산됩니다.

따라서 8개의 숫자에서 6개의 숫자를 선택하는 방법은 총 28가지가 있습니다. 각 조합을 구체적으로 나열하면 다음과 같습니다.
1, 2, 3, 4, 5, 6, 7, 8에 각각 자신이 고른 8개의 번호를 대입시키면 로또 완전조합이 됩니다.
예를 들면 12, 13, 18, 20, 27, 33, 34, 40라는 숫자를 고르면 1-12, 2-13, 3-18, 4-20, 5-27, 6-33, 7-34, 8-40 에 대입시키면 됩니다.
1. {1, 2, 3, 4, 5, 6}
2. {1, 2, 3, 4, 5, 7}
3. {1, 2, 3, 4, 5, 8}
4. {1, 2, 3, 4, 6, 7}
5. {1, 2, 3, 4, 6, 8}
6. {1, 2, 3, 4, 7, 8}
7. {1, 2, 3, 5, 6, 7}
8. {1, 2, 3, 5, 6, 8}
9. {1, 2, 3, 5, 7, 8}
10. {1, 2, 3, 6, 7, 8}
11. {1, 2, 4, 5, 6, 7}
12. {1, 2, 4, 5, 6, 8}
13. {1, 2, 4, 5, 7, 8}
14. {1, 2, 4, 6, 7, 8}
15. {1, 2, 5, 6, 7, 8}
16. {1, 3, 4, 5, 6, 7}
17. {1, 3, 4, 5, 6, 8}
18. {1, 3, 4, 5, 7, 8}
19. {1, 3, 4, 6, 7, 8}
20. {1, 3, 5, 6, 7, 8}
21. {1, 4, 5, 6, 7, 8}
22. {2, 3, 4, 5, 6, 7}
23. {2, 3, 4, 5, 6, 8}
24. {2, 3, 4, 5, 7, 8}
25. {2, 3, 4, 6, 7, 8}
26. {2, 3, 5, 6, 7, 8}
27. {2, 4, 5, 6, 7, 8}
28. {3, 4, 5, 6, 7, 8}
이 조합들은 모든 가능한 6개의 숫자 선택을 포함합니다.

5. 조합의 활용 예시
1) 로또 번호 선택
로또 번호를 선택할 때, 위의 방법을 사용하여 8개의 숫자에서 6개의 조합을 만들 수 있습니다.
이를 통해 모든 가능한 조합을 검토하고, 자신에게 맞는 조합을 선택할 수 있습니다.
2) 통계 샘플링
통계학에서 데이터를 분석할 때, 다양한 샘플을 선택하는 것이 중요합니다.
8개의 데이터를 가지고 6개의 샘플을 선택하여 다양한 분석을 수행할 수 있습니다. 이는 샘플의 대표성을 높이고, 분석의 신뢰성을 증가시킵니다.
3) 퍼즐 게임
숫자 조합 퍼즐 게임에서, 8개의 숫자에서 6개의 숫자를 선택하여 퍼즐을 풀어야 하는 경우, 위의 조합 방법을 사용하여 모든 가능한 조합을 검토할 수 있습니다.
이는 퍼즐을 푸는 데 필요한 다양한 시나리오를 제공하여 해결책을 찾는 데 도움이 됩니다.
4) 마케팅 분석
마케팅 전략을 세울 때, 다양한 요소들의 조합을 고려할 필요가 있습니다.
예를 들어, 8개의 마케팅 요소 중에서 6개의 요소를 선택하여 캠페인을 구성하는 경우, 가능한 모든 조합을 검토하여 최적의 전략을 찾을 수 있습니다.
6. 조합을 이용한 문제 해결
조합을 사용하면 다양한 문제를 해결할 수 있습니다. 예를 들어, 특정 조건을 만족하는 조합을 찾는 것이 필요할 수 있습니다.
이러한 경우, 조건에 맞는 조합만을 선택하는 필터링 기법을 사용할 수 있습니다.
예를 들어, 6개의 숫자의 합이 특정 값이 되도록 하는 조합을 찾는 경우, 모든 조합을 계산한 후 합이 해당 값이 되는 조합만을 선택할 수 있습니다.
또한, 조합을 사용하여 확률을 계산할 수도 있습니다.
예를 들어, 8개의 숫자 중에서 6개의 숫자를 선택할 때, 특정 숫자가 포함될 확률을 계산할 수 있습니다. 이는 조합의 수를 사용하여 확률을 계산하는 기본적인 방법입니다.

마치며
8개의 숫자에서 6개의 숫자로 완전 조합을 만드는 것은 다양한 분야에서 유용하게 활용될 수 있는 수학적 개념입니다.
이를 통해 로또 번호 선택, 통계 샘플링, 퍼즐 게임, 마케팅 분석 등에서 최적의 전략을 찾을 수 있습니다.
조합론의 기본 개념과 활용 방법을 이해하면, 복잡한 문제를 보다 효과적으로 해결할 수 있습니다.
관련글 더 보기
7개 숫자로 로또 완전조합 만들기
로또는 '운명'이라는 뜻의 이탈리아어 '로토'에서 유래한 복권의 일종입니다. 사람들이 로또를 구매하는 주된 이유는 경제적 안정과 부유함을 얻고 싶어서입니다. 로또 당첨금은 삶을 완전히
diamondstock0509.tistory.com
로또 1등 당첨자 63명 역대 최다 기록 경신 및 당첨금 세금
2024년 7월 13일 추첨된 제1128회 로또 복권에서 1등 당첨자가 63명이 나오면서 역대 최다 기록을 경신했습니다. 이번 1등 당첨금은 1인당 약 4.2억 원으로, 역대 두 번째로 낮은 수준입니다. 1. 1128
diamondstock0509.tistory.com
'돈과 경제' 카테고리의 다른 글
| 로또 9개 숫자로 6개 완전조합 확률과 경우의 수 (0) | 2024.08.18 |
|---|---|
| BNK경남은행 3000억 원대 횡령 사건 징역 35년형 선고 (0) | 2024.08.09 |
| 로또 1등 당첨자 63명 역대 최다 기록 경신 및 당첨금 세금 (4) | 2024.07.14 |
| 정부 소상공인 금융 비용 성장 지원 종합대책 발표 (2) | 2024.07.09 |
| 항공권 더 저렴하게 구매 하는 9가지 꿀팁 (0) | 2024.06.29 |



